PICTURES, MODELS AND MEASURES by Susan G. Sterrett (Tractatus Odyssey Chapter)

This paper is based on the paper of the same title presented at the 2015 Pacific APA Meeting, Vancouver, BC April 1–4, 2015 in the Invited Symposium: ‘Wittgenstein’s ’Picture Theory’’ 1 pm Friday, April 3rd.

PICTURES, MODELS, AND MEASURES

Susan G. Sterrett

Department of Philosophy, Wichita State University

Abstract. In this paper, I enrich the context of Wittgenstein’s Tractatus given over a decade ago in my book Wittgenstein Flies A Kite (and related earlier works dating from 2000). I’ve since located a sketch reprinted from a 1914 Paris magazine showing a lawyer using a model bus and dolls to depict a traffic accident; I present it here along with a discussion of the modelmaker movement of that time. Th e modelmaker movement was a movement at the intersection of popular culture and technical expertise that really needs to be understood and recognized in discussing Wittgenstein’s use of Modell and Bild. I discuss its role in relation to experimental models used in scientific research. Other new aspects presented here include: the very special role of model-flying clubs (known in Germany as Modell-Flugverein); the use of scientific forensics in courts of law, really just beginning then (c. 1914), and a part of popular culture as well; the significance of more recent work by others on Boltzmann’s personal interest in flight, and on the widespread but now-forgotten discussion of dimensional analysis in the history of physics. I conclude that all these lend support to the views on the Tractatus I laid out in my book, and summarize and elaborate on some of them here, inasmuch as space permits. More generally, I argue that the philosophical community interested in interpreting Wittgenstein’s early works stands to gain from becoming better acquainted with the scientific and technological developments of the milieu in which they were conceived.

 Introduction

The Tractatus was completed almost one hundred years ago. That is recent enough that readers tend to feel comfortable taking the terminology of pictures, models, and yardsticks to have the connotations familiar to us today. Many commentators rely on their own familiarity with the terminology of pictures, models and yardsticks when discussing the text. This is likely attributable to lack of better options: Wittgenstein directed that all his books and papers were to be disposed of when he left Cambridge, so there is little to go on from that early period, in terms of his personal effects. Another shortcoming in historical sources commonly consulted by academics writing on early 20th century analytic philosophy is that history of science and technology has not been as integrated into philosophy as, say, history of logic and literature has. Though lack of his personal effects may be the reason for looking to Wittgenstein’s milieu for the contextual cues in reading his works, in general I think there is something of value to be gained in looking at the context specific to an author at the time they wrote a text, anyway. The availability of materials following the massive digital archiving of magazines, newspapers, and journals that has occurred in the last two decades now makes it possible to bring things into discussion that were not as convenient to locate a decade or two ago.

My hope in this paper is to enrich discussion about pictures, models and measures in the Tractatus by providing context about technology and science in the life of the author of the Tractatus (e.g., circa 1889–1919). Situating his remarks and works in that landscape should yield a more complete account of what was being said, and thus aid in sorting out some puzzling passages and themes.

Situating This Paper

There have of course already been some works that consider the contribution that research in intellectual history might add to understanding the Tractatus, and some of these tend towards the scientific and technical. McGuinness researched Wittgenstein’s years studying engineering: at the Technische Hochschule (THS) in Charlottenburg near Berlin, at the Kite-Flying Station in Glossop near Manchester, and at what is now the University of Manchester, where he was enrolled as a research student in aeronautical engineering. McGuinness identified the courses in Descriptive Geometry and Graphical Statics taught at the THS as important to Wittgenstein’s idea of the proposition as picture. (McGuinness 1988/1995, p. 61) Janik & Toulmin (1996) explore overarching intellectual movements in Vienna, including art and music[ii]. What my contribution here provides in terms of historical context is somewhat more specific to the interests and situation of the author at the time in his life when he wrote the Tractatus, but it is in the same spirit of providing context for that work. I believe the work presented here pulls the curtain on something that was ubiquitous in science and technology at the time, but has since disappeared from view—certainly from the view of most philosophers and philosophers of science today: the language of dimensions, sometimes referred to as dimensional analysis or the theory of dimensions.

There has been some recent work in philosophy on the history of the concept of dimensions in science, however, hopefully portending a resurgence of interest. (Mitchell 2017; de Clark 2016, 2017; Walter 1990) This element of Wittgenstein’s milieu—dimensions (in the sense of dimensional analysis and dimensional equations) was often referred to as the language of science at that time (as opposed to the current tendency to confer that status on logic, set theory, model theory, or differential calculus). I first presented my own speculations on an interpretation of the Tractatus in which the puzzling account of objects in the Tractatus becomes clear when seen on analogy to dimensions, in a submission to HOPOS 2000 in Vienna in late 1999; it appeared the following July in the book of abstracts for the HOPOS 2000 program[iii] I gave a short version of the paper at HOPOS 2000 and a longer version later that year titled: ‘Physical Pictures: Engineering Models circa 1914 and in Wittgenstein’s Tractatus.’ (Sterrett 2000) At the time I offered it as an original and unprecedented suggestion, somewhat speculative, resulting from many years of thinking about the methodology of scale models and the Tractatus. It was speculative in the sense that the interpretation of the text had come first; searching for historical evidence afterwards.

Subsequently, i.e., over the last twenty years, I have delved further into both the history and the philosophy of the concept of ‘physically similar systems’ and the theory of dimensions. (Sterrett 2006; Sterrett 2009; Sterrett 2017a; Sterrett (forthcoming a)]. I can say without reservation that all this further work made the suggestion seem far less speculative than when I initially presented it. The few unconnected historical bits that I had to go on when I first presented at HOPOS 2000 on the role of dimensional analysis and scale models in the scientific and technical milieu in which Wittgenstein conceived and wrote the Tractatus, were merely to establish the existence of the methodology of experimental scale models (physically similar systems) at the time, and show it was part of his world. This has since been supplemented to give a somewhat fuller account of the cultural ubiquity of other kinds of scale models, clarifying the role of experimental scale models among other kinds of scale models of that time, their especially tight connection to the history of flight in the year 1914, and indications that Wittgenstein not only would have been well placed to appreciate their role, but that he most likely did in fact have such an interest. In addition, some recent work on the history of dimensional analysis by others now makes it clear that Wittgenstein’s interest in physics (as opposed to engineering) during his youth was another possible source of knowledge of the theory of dimensions. (Mitchell 2017; de Clark 2016; 2017; Buchwald 1994, p. 200ff; Walter 1990, Ch. 4) Though my initial analogy between dimensions in science and objects in the Tractatus did not crucially depend on any particular historical claims, it turns out that all the above support the suggestion that the theory of dimensions and the notion of physically similar systems were relevant to Wittgenstein’s interests.

Pictures and Models

While many have attributed a ‘picture theory’ and/or ‘Bildtheorie’ to Wittgenstein, I am not aware of Wittgenstein ever having used the term ‘picture theory’. What I have noticed is that there is a point in time before which Wittgenstein does not use the word often translated as ‘picture’ (Bild) in connection with a proposition; but that, after that point, the word and its cognates appear frequently in his writings. They occur not only in his writings in the weeks immediately afterwards; many works written even decades later feature ‘picture’, both as a verb [abbilden, tr. as depict] and as a noun [Bild, tr. as picture].

That point in time—i.e., the point in time before which Wittgenstein does not use the word ‘picture’ in connection with a proposition, and after which he frequently does so—is recorded in the notebooks he kept while serving in the military, so we know the date (September 29, 1914), and we know what, according to him, occasioned the insight he regarded as so crucial. We know this not only from the notebook entry itself, but from the fact that he recounted the vivid memory he retained of the occasion on which he had this pivotal insight to several friends, multiple times. (von Wright n.d., p. 20 fn. 9; p. 20–21) What occasioned it, he said, was reading about the use of physical miniatures (‘Puppen’)—a miniature model—to portray a traffic accident in a courtroom. The description itself found in the notebooks, made on the day he recorded the occasion, actually appears very unassuming on its face, in itself giving no sign of the importance he seemed to later place on it, as it is placed inside parentheses. After ‘In the proposition a world is as it were put together experimentally’ [Im Satz wird eine Welt probeweise zusammengestellt.] he puts in parentheses the following phrase: ‘As when in the law-court in Paris a motor-car accident [Automobilunglück] is represented by means of dolls [Puppen], etc.’ Though, that he had some sense of the importance he expected it to hold for his project is indicated in a note that follows directly after: ‘This must yield the nature of truth straightaway (if I were not blind.)’ (p. 7)

If Wittgenstein is talking about physical objects like dolls, as it seems he is, you would expect him to talk about models rather than pictures. David Stern’s commentary is helpful here: regarding the use of ‘picture’ rather than ‘model’ in the term ‘Picture Theory’ that is used by so many commentators, Stern explains: ‘Wittgenstein used the word ‘Bild’ to talk about the model, a term usually translated as ‘picture’; […] While both words cover such things as images, film frames, drawings, and paintings, the idea of a three-dimensional model is more readily conveyed by the German ‘Bild’ than the English ‘picture’. (Stern 1995, p. 35–36) However, I would amend Stern’s comments, in a way that does no damage to his point, with the recognition that we actually do in fact see Wittgenstein use the word model, too—notably, to relate Bild and Model. This is in T 2.12: ‘A picture [Bild] is a model [Modell] of reality.’ [Das Bild ist ein Modell der Wirklichkeit.] Stern is not the only major commentator on Wittgenstein who seems not to notice this line of the Tractatus, though, so I would like here to highlight the fact that in the Tractatus there is this explicit use of the word ‘Modell’ in the German text; thus the occurrence of the word model in various English translations of Tractatus T 2.12 is not solely a matter of the translator’s choice of how to interpret the term ‘Bild.’ In T 2.12, then, Wittgenstein is relating Bild to Modell [of reality]. This is in line with Stern’s view, i.e., that the picture theory ‘involves generalizing from what models, pictures, and the like are supposed to have in common, and treats two-dimensional pictures as just one kind of Bild.’ [Stern, Mind and Language, p. 36]

Instead of relying solely on notions of model readily available to us, we can also look at the context in which Wittgenstein wrote this. I don’t mean where Wittgenstein was located physically, but the cultural context in which the German word Modell ought to be interpreted: How was the word used then? What connotations were associated with the word then? A look at the usage of the term ‘Modell’ at the time Wittgenstein wrote this line in the Tractatus shows that in the late nineteenth and early twentieth century it was often used in conjunction with models of machinery, including steam boilers, engines, and automobiles, and that by 1914 it had become used frequently in association with model airplanes. And, in fact, as I’ll show below, when used in conjunction with airplane, Modell took on additional connotation: airplane models were used not just as models to inform, illustrate, and delight, but as experimental models meant to advance research. It is anachronistic to look at the role experimental models have in scientific and technical practice today, however. Interest in miniature models of machinery was a cultural phenomenon: there were clubs that eagerly sought the membership of young people still in school as well as of distinguished scientists; there were well attended public competitions and exhibitions reported on in newspapers, and magazines devoted to the topic flourished. The magazines featured vendors providing specialized products for the activity of building and furnishing models. Some even thought of it in more epic terms, as a movement. It cut across social classes, countries, disciplines, and professions.[iv]

For context here, I look, not just at a particular point or period of space and time, but at how Wittgenstein navigated through the various opportunities the world presented to him. His interest in design and construction of airplanes is consistent over many years. This is known largely from comments reported by others. McGuinness, who spent many hours interviewing family, friends, and acquaintances of Wittgenstein, writes that his sister said of Wittgenstein’s interest when he made the choice to go to England to do research at the Kite- Flying Station in Glossop and study engineering in Manchester to long after: ‘As long as he worked in aeronautics at all, his aim seems to have been to design, build and fly a machine himself ’. (McGuinness 1988/2005, p. 69) He mentioned his strong interest in aeronautics to Russell even after he had left engineering study at Manchester. It appears that he still had some interest in engineering while at Cambridge studying logic. We know this due to a letter of Russell’s. In managing the collection of Wittgenstein’s books and papers he’s received, which he had agreed to buy when Wittgenstein had decided to dispose of them, he writes to Wittgenstein asking him what he ought to do with his parcels from engineering firms, at least some of which I take to be printed materials. [Wittgenstein in Cambridge, Letter No. 90, p. 127] Even though Wittgenstein had his books disposed of in 1914, they were not destroyed nor lost to posterity; rather, Russell kept at least some of them. From Russell’s collection, we know that among the books Wittgenstein had while he was in Cambridge were many about the history of flight, as explained below.

Other indications of the context that is relevant to Wittgenstein’s early thought and writings are the desires he had about where and what to study. In 1906, Wittgenstein had wanted to study with Boltzmann, and biographers have assumed it was his interest in physics that explains this desire. However, when Boltzmann died that year, Wittgenstein went to the Technische Hochschule (THS) in Charlottenburg near Berlin to study engineering, not physics. Oystein Hide, who identified, catalogued and reviewed the set of books in the Russell archive thought to have belonged to Wittgenstein (2004) believes that many of the books on the history of flight that we know of in that collection were purchased from an antique bookseller during the time Wittgenstein was a student at THS. This independently indicates that Wittgenstein had an ardent interest in flight at the time, an interest we know continued in the years to follow as he left Vienna to move to and study in England. And, the visits to antique booksellers to purchase books on the history of flight indicates that he fed that interest in activities outside of the formal school day. Wittgenstein seems to have regarded his experience at the THS as a waste of time. Knowing how he spent his time outside of formal school classes, we can attribute to him both a lack of interest in his engineering classes at THS and an ardent interest in designing, building and flying an airplane.

Wittgenstein’s interest in flying as a boy does not need any special explanation, as it was a very common interest for a boy at that time. But the form that interest took—the kinds of books he bought, his huge decision to move to England to pursue flight research in spite of his poor grasp of the English language, and his interest in spending months in a relatively isolated location doing research at the Kite-flying station—is somewhat singular. Here, it seems to me, Boltzmann’s interest in and advocacy of flight research may well have played an important role—as McGuinness also implies (McGuinness 1988/2005). Boltzmann’s ‘On Aeronautics’ was a major lecture delivered to one of the most important societies for scientific research. It was a well-attended public lecture given near Wittgenstein’s family’s home in the Alleegasse in 1895, when Wittgenstein was six years old, was reported on in the newspaper afterwards, and reprinted in early editions of the German editions of his Populäre Schriften. I provided an English translation (‘On Aeronautics’) as an appendix to my book, as no English translation of it was available.

Boltzmann stressed the value of studying kites in flight, presenting kite flying as crucial scientific research that could be carried out using a child’s toy. What is interesting is Boltzmann’s remarks on the relative superiority of England over Germany with regard to their expertise in experimental models. As I noted (Sterrett 2006), when Boltzmann was asked to write an encyclopedia article on Modell, he tried to refuse the request and suggested that instead the editor ought to get someone from England, where there are experts on models. (Blackmore 1995, p. 57) It is also worth noting that Boltzmann talks specifically about models of flying machines, and what he says about them is significant: ‘A distinction must be observed between the models that have been described and those experimental models that present on a small scale a machine that is subsequently to be completed on a larger, so as to afford a trial of its capabilities. Here it must be noted that a mere alteration in dimensions is often sufficient to cause a material alteration in the action…’

What Boltzmann describes here is the kind of model that, unlike many other scale models, is an experimental scale model. Then he goes on to say that, unlike the previous models he has been describing and making observations on, these are different—in how they serve as models, and in the considerations for constructing them—and he explains that the theory behind understanding how experimental (scale) models are to be constructed is the theory of dimensions: ‘… the various capabilities depend in various ways on the linear dimensions. Thus the weight varies as the cube of the linear dimensions, the surface of any single part and the phenomena that depend on such surfaces are proportionate to the square, while other effects—such as friction, expansion and conduction of heat, &c., vary according to other laws. Hence a flying machine, which when made on a small scale is able to support its own weight, loses its power when its dimensions are increased. The theory, initiated by Sir Isaac Newton, of the dependence of various effects on the linear dimensions, is treated in the article Units, Dimensions of.’ (Boltzmann 1974, 220)

Boltzmann’s mention of Isaac Newton in connection with experimental models of flying machines explains an anomaly in Oystein Hide’s catalogue of Wittgenstein’s books at the Bertrand Russell Archives. I noted that Wittgenstein obtained a copy of Newton’s Principia.; this is very plausibly due to Boltzmann making the point he did about Newton in this lecture, of which Wittgenstein was almost certainly aware. Wittgenstein also obtained a copy of Galileo’s Two New Sciences, a precursor to Newton’s writings on the problem, which discusses the problem of experimental scale models in almost the same terms that Boltzmann put it: in Galileo, a support structure for a ship when built on a small scale, loses its strength when built in the same proportions but of a larger size. These two purchases are anomalous; there aren’t other books of that sort among his collection. Wittgenstein owned no other books by Galileo, and the book he bought, an English translation of Two New Sciences was very rare, difficult to find, and costly. [see Sterrett 2006, p. 130–131] I speculated that Wittgenstein’s interest in these rare books was due at least in part to Boltzmann’s remarks in his encyclopedia entry ‘Modell’, since Boltzmann mentioned Newton’s theory of dimensions as the basis for understanding scaling, and it is well known that Galileo also takes up the topic in Two New Sciences. If Boltzmann’s advocacy of flight research—he was concerned that Germany was behind other nations—was salient in Wittgenstein’s life, it would explain the path Wittgenstein navigated: first trying to study with Boltzmann, then studying engineering in Germany, but leaving for a country considered better suited to make advances in flight research at that time: England. I also noted that Boltzmann’s formulation of the problem reiterated and reinforced the way the problem of heavier-than-air flight was presented in Jules Verne’s Robur the Conquerer in German (Clipper of the Clouds in England) which was very popular among boys of Wittgenstein’s generation.[v] I also discussed the role of Viennese engineer Otto Lilienthal in the history of flight and in Wittgenstein’s boyhood milieu. (Sterrett 2006, Ch. 2) Lilienthal’s fame has stood the test of time and he is widely recognized as a pivotal figure for his human gliding experiments.

It turns out that Boltzmann’s interest in flight was even more intense and practically oriented than I had realized: Boltzmann and Lilienthal knew each other. Dahmen (2007) has devoted an entire article to the topic of Boltzmann’s advocacy of research into heavier than air flight. He presents and reviews the correspondence between Ludwig Boltzmann and Otto Lilienthal. Boltzmann evidently was interested in purchasing a glider from Lilienthal and it sounds like he was planning to carry out research using it himself. Thus Boltzmann’s remarks about the theory of dimensions explaining the behavior of experimental models of a flying machine in his article ‘Model’ are more than a disinterested observation about the methodology of models; he may have been thinking of staking his safety on it. The last line of that essay, about the solution to the problem of flight requiring someone who is not only a genius, but also a hero, could allude to the need for such personal risk-taking.

The remarks Boltzmann made in his article on models for Encyclopedia Brittanica then take on much more significance. In summary, he made these important points: (i) It is not correct to think of experimental scale models of flying machines in the same manner as the other kinds of models he discusses. For the other kinds of models he discusses, he said, ‘it is perfectly clear that these models of wood, metal and cardboard are really a continuation and integration of our process of thought.’ But experimental models cannot be regarded this way, he says. Thus the view of models as ‘a continuation and integration of our process of thought’ is not the proper account of the methodology of experimental models. Rather, (ii) the methodology of experimental scale models of flying-machines is the theory of dimensions. Importantly, he goes on to say that (iii) experimental scale models include not only models in which mechanical forces are involved, but ‘models of thermal, electro-magnetic and other engines—e.g. dynamos and telegraphic machines. This naturally invites the question as to whether the method used for experimental models of flying-machines, i.e., the method of dimensions we find the beginnings of in Newton, might be extrapolated from mechanics to thermodynamics and electrodynamics, and, even, generalized so as not to be specific to any particular physical phenomena.

The Model Engineer

None of the biographical work on Wittgenstein indicates that models of airplanes had a role within the THS school curriculum, and Wittgenstein later spoke of his education there as being of little value. Yet, there was more to intellectual life than school. Did his hours outside school include model building? It is hard to answer this for his specific years at THS, but it is known that he built a model of a sewing machine (McGuinness 1988; p. 45; 178) while quite young, and that he was known at school for having a model airplane. The significance of model airplanes to the epic problem of heavier-than-air flight was that some, but not all, of them were successful examples of heavier-than-air flight, and the ones that were successful could actually be set in competition with each other, experimentally. Model airplanes powered by large, strong rubber bands could fly for extended periods (on the order of a minute or longer).[vi] The model of a sewing machine was a working model as well. As Boltzmann indicates, the experts on making models were to be found in England. But what kind of expertise is he talking about here; is he talking about expertise in making the kind of models that Wittgenstein would have had as a boy, e.g., airplane models and models of sewing machines to be constructed by hobbyists?

You might wonder why a distinguished physicist writing an encyclopedia article would even take note of the skill of hobbyists or the expertise involved in a toy-maker’s craft. But it is anachronistic to use the kind of categories we’d use to characterize models now, such as toy versus scientific model, to describe the models of the late nineteenth and early twentieth century. In that encyclopedia article on models, Boltzmann mentions the model collection in the US Patent Office; these would in most cases be working models of the machines for which a patent was sought, though they would not necessarily be models used for scientific and technical research.[vii] The goal would be to illustrate how the machine worked; thus some scientific knowledge would be drawn upon in designing the model to ensure that it would work in a way that illustrated how the larger machine being modeled worked.

One manifestation of the cultural status of models is the magazine Model Engineer begun in 1898 in the UK, and still being published today. What was modeled? Boats, of course. But also steam boilers. Engines of every kind. Windmills. Tractors (‘Traction Engines’) Railway cars for all sorts of specialized purposes. Screw Propellers. Automobiles, too. These kinds of models often aimed to please the eye as well as to illustrate how the machine operated; thus, they usually reflected the proportions of the thing modeled, at least for the visually prominent outlines. A few examples to illustrate how the art of crafting small objects was intermixed with the employment of mechanical principles may be helpful here in evoking the context in which the word model was used circa 1914. First, here is an entry about a model boiler from the magazine The Model Engineer and Electrician in 1908, that illustrates that ‘working model’ was taken in an extremely literal and precise sense: here, the author is proud of the fact that the efficiency of the model boiler is so close to the efficiency of the boiler it models.

Many models were propelled by engines that really operated; often various types of substances found in the household could be used as fuel, such as paraffin or alcohol. The engines burned the fuels and the processes inside them were very like full-sized engines, operating at high pressures, as shown by the following article about providing safety valves for your toy model engines:

These magazines featured original (i.e., only one was made) handmade models with descriptions of the materials, processes and tools used. Model hobbyists shared their experiences and advice, but some items, such as model boilers and model engines, required so much work and practice to get right that they were manufactured for sale to hobbyists for use in their constructions, too. A model toy engine might propel a boat, or a tractor, or even an automobile. The 1908 Model Engineer and Electrician prominently featured a model automobile; the wheels are 3 inches in diameter, and the automobile is 13 inches long and over 7 inches high.

As Boltzmann noted, experts in constructing small models of machines could easily be found in England; the implication is that one would have trouble doing so in Germany or Austria at that time. The movement in England spread to the US, too, with model clubs, exhibitions, and magazines thriving there, too. Once one knows what to look for, examples of this cultural phenomenon can probably be found in any number of places. For example, in a recent biography of Ann Dunham, mother of President Barack Obama, we read that her great-great grand-uncle Frank W. McCurry, born in 1893 (four years after Wittgenstein), who ‘climbed derricks as a child in Peru [Kansas] and went on to become a pharmacist, a chemical engineer, and an oil company vice president, acquired a certain degree of fame, as an adult, for an unusual hobby. Over forty-five years, he built, fine-tuned, and continually updated a fully functioning scale model of an oil refinery, made largely out of glass. The model refinery, which had two catalytic cracking units and actually produced gas from oil, traveled to high schools and colleges all across the country’. (Scott 2011) Such accomplishments encountered in isolation from the model engineer community appear as quirky personal interests, but making exquisite working models of complex machinery was not in fact such an unusual hobby in the US and the UK during the early twentieth century.

In some fashion, the movement spread to Europe, too: In the June 1914 issue of Popular Mechanics, it is reported that ‘there is a famous German model shop in which exquisite miniatures of bridges, boats, steamers and models for demonstration and experimental purposes are made’. Besides the report on steamboats made for exhibition, there is this amazing news: ‘A model of a universal rolling mill for I-beams, with a capacity for beams up to 40 in. high, was recently made in this shop, and the little model was so perfect that machine-steel billets could be rolled into I-beams only 3/4-in. high. Bridges, lifts and intricate machinery which cannot well be installed for exhibition purposes are shown in miniature, and this firm is kept busy, orders coming to it from all parts of the world.’ [‘Miniature Models Made in Big Shop’ Popular Mechanics, June 1914.]

By 1914 the idea of a child making miniature models, rather than merely playing with them, appeared in an advertisement in Popular Mechanics: ‘Say Fellows! Build the Brooklyn Bridge … in your own home—build it like real engineers with real solid steel girders, beams, plates, bolts and nuts…. Build traveling cranes, elevators, towers, aeroplanes, power derricks, Ferris wheels, printing presses and automobiles that really run and work—build all your own toys …’

Recalling Boltzmann’s point about why experimental scale models are different than other kinds of models that we use as ‘a continuation of our thought’, i.e., that an experimental model that works when built at one size may not work when using the same proportions but built of a different size, we can see that often a model builder would have to take into consideration factors other than just those needed to scale the linear dimension of the model, if the goal was a working model. Yet these were still not experimental (scale) models in the sense needed for scientific research. In the mind of someone who pondered the relationship between miniature machines and the machines they modeled, the model engineer movement might occasion the same question that was so fundamental to solving the problem of heavier-than-air flight: how to scale up from the model to a full-size machine—but the model engineer hobbyist would not really need to solve that general question in a rigorous manner. Ad hoc measures for a specific model, used in conjunction with scientific and technical knowledge, trial and error, and sharing of information via clubs and magazines, was in many cases enough to produce models that performed as intended.

Not all, however: a recurring theme in the magazine was controversies over how to design the screw propeller for a model marine vessel. And flying machines were enough of an exception that those interested in model flying machines often formed their own clubs.

Although the model engineer movement was strongest in the UK and the US, we have seen that there was a shop selling these highly engineered working models of machines and machinery that had achieved fame and was flourishing in Germany by 1914. Another movement in Germany around that time was the interest in building and flying model aeroplanes. An article entitled ‘Modell-Flugvereine’ [Model Flying Clubs’] in the Deutsche Luftfahrere Zeitschrift of December 20, 1916, gives an account of this cultural phenomenon in Germany[viii], from which I quote:[ix]

It is well known that our earliest and first designers and aviation pioneers, such as Lilienthal, Etrich, Langley, Chanute, Wright and others, experimented with their ideas on models and gained their first experiences through various and iterated model constructions.

In many cities of the German Reich, a movement that began in 1912 led to the founding of clubs whose members were concerned exclusively with the construction of model airplanes. Not for entertainment or play, but for teaching younger members: to teach them about the concept of ‘heavier than air’ aircraft, in order to help them develop a proper understanding of the construction of such aircraft. And for them, upon understanding, to give older members fresh suggestions for continuing their experiments, when daunting failures occurred, as they often do, when trying out a new model.

How this building of aircraft models and the association of modelmaking supporters in clubs with each other increased the personal knowledge of each individual and enabled them to accomplish what would undoubtedly not have been so quickly and effectively achieved without these studies on models, is becoming revealed in this war, in a fortunate way. It is a commendable fact that, with very few exceptions, almost all members of model clubs that have been drafted or joined as war volunteers serve in the Air Force, where their service excels, both among the aviation troops and the aircraft pilots. Others found recognition of their abilities in technical service. Their prior knowledge shortened their training and facilitated their understanding and their ability to absorb new technical difficulties. The value of model making is evident here. However, a lack of education and orientation of the public eye—and, an unfortunately often intentional lack of regard for this field of expertise on the part of many experts—can lead to a misjudgment of the value of modeling.’

Wittgenstein left Manchester in 1911 for Cambridge, which is before the movement took shape, according to this article; however, between 1911 and the summer of 1914, he made trips back to Vienna numerous times. In fact, he spent time in Vienna in July 1914. (This is based on the return address of his letter to G.E. Moore from that visit.[x]) When he requested to join the military, he had hoped to be assigned to the part of the military that had to do with aeronautics, which, at that time, was located in the Balloon division.[xi] It is more than plausible that he would be interested in the existence of this Modell-FlugVereine movement and, given his family connections, and his experience living in Germany while studying at the THS, that he would be able to learn of its existence and a little about its activities.

The Model in Law-Court

As explained above and in previous work, my own evaluation of the role of the event Wittgenstein placed so much emphasis on—of the miniatures being used in a courtroom to portray a traffic accident—is that intellectually the moment was more a matter of Wittgenstein’s recognition that he had come across what he had been looking for, than it was a brand-new realization or a moment of transformation. That is, I believe that the moment was significant, but that the significance it held was more like the significance of an artist or writer coming across just the needed item or inspiration to proceed with their efforts, as opposed to the significance of a moment of conversion dislodging an opposing view. That is—as I think is often the case with sudden insights—I think that Wittgenstein’s ideas about propositions had already been developing, and seeing the use of miniatures to depict an accident used by a lawyer in a law court suddenly gave him a metaphor or a way of organizing those thoughts in an especially perspicuous way. The way I described it in my book was that, when he had an insight occasioned by the magazine article’s description of a miniature setup used in a law court that served up to him what he needed to formulate his thoughts about the proposition-as-a-picture and picture-as-a-model, it was like the recognition a sculptor has in lighting on an appropriate item to use as a found object in a sculpture already partially envisioned. (Sterrett 2006, p. 251–252)

A great many people have written about Wittgenstein’s reading of the use of miniatures in the courtroom. According to von Wright’s memoirs, Wittgenstein mentioned it to many friends on many different occasions (von Wright, n.d. 20 fn 9); no one, so far as I am aware, has ever located the newspaper account or the court case about the traffic accident that occasioned his insight. My concern, however, has been, not that the newspaper account has so far not been located, but that these discussions have not put the use of miniatures in the courtroom in their historical context. The context of the history of science and technology is especially relevant here, for it reveals that there was a time when miniatures were not just toys, but scientific objects. As for the depiction of the use of models of a traffic accident in a magazine, I have, in spite of the expenditure of an inordinate amount of time on fruitless efforts to locate it, finally happened upon something close to it: a magazine account of the use of a miniature car and bus to depict a traffic accident, which was published in 1914. This is consistent with a report that Wittgenstein, much later, spoke of seeing ‘a newspaper notice which said that in Paris at a legal proceeding about a traffic accident, the accident was presented with dolls and a little bus.’ (Klagge 2016) The sketch of the lawyer using the miniatures is credited to a French publication published in Paris (L’Illustration). It is striking that the mention of dolls and a little bus match this illustration, too. I cannot be certain, in the sense historians demand, that it is the same depiction of what happened in the lawcourt or even that it depicts the same accident, but I think it is at least fair to say that the illustration and accompanying text depict the sort of use of miniatures in a courtroom that was a newsworthy practice in 1914.

The caption on the illustration reads: ‘Reproducing a Traffic Accident in a Lawyer’s Office’ and the accompanying text, a brief news item, is: ‘LAWYER STUDIES ACCIDENT WITH PLAT AND TOYS. A London lawyer, who specializes in personal-injury litigation, in studying a case to place the responsibility for the accident, and obtain a clear idea of the different phases of the affair, reconstructs the whole occurrence on a plat or plan of the locality, placing miniature vehicles representing the parties in such position that the questions of right of way, traffic regulations, rules of the road, and such matters, are clearly shown. Thus equipped, he is able to place his case lucidly before the court.’

The illustration depicts a bus that has collided with a smaller wheeled vehicle in the intersection of a road. Three other vehicles are shown approaching the same intersection. Several things are notable about the news item. First, it mentions that the lawyer is interested in ‘the different phases’ of the accident. In the case of a collision, this would mean the lawyer is interested in the relative positions of the vehicles and their trajectories before, during, and after the point in time that the vehicles collided. Second, it mentions that the lawyer reconstructs ‘the whole’ occurrence and does so in a specific context, ‘a plat or plan of the locality’. Some of the large sheets of paper on the table the lawyer is working on are raised in relief, simulating hilly terrain that blocks the view of the two vehicles approaching the intersection from each other. Thus the lawyer would be interested not only in the trajectories of motion of the center of motion of the vehicles as they approached the intersection before colliding, but in the trajectory of all the visible points on the vehicles, and their relation to the line of sight of the occupants (dolls) in the vehicles.

The way of using the model setup pictured I have just described is not quite the same as using the models as experimental models scientifically, or as experimental engineering scale models; that would require one more step: designing the setup so that the model setup and the actual setup it models are physically similar systems (i.e., similar in the sense of a certain kind of behavior such as kinematic behavior (same motions and velocities), or dynamic behavior (same forces)). The kind of behavior relevant here would be behavior relevant to some claim important in the trial. As explained in (Sterrett 2006, 2009, 2017a, and 2017b), to say that two setups are physically similar systems is always with respect to some specific behavior, and the behavior of interest here would depend on the claims in the lawsuit. If the claims in the lawsuit turned on a measurement such as how fast a car was going, or how much impact force the victim sustained, the kinds of similarity would be kinematic similarity and dynamic similarity, respectively.

Before and After 1914

My views on the nature and significance of the event occasioned by reading about the use of miniature models in the courtroom are informed by looking at various elements of Wittgenstein’s milieu that provide the context in which Wittgenstein viewed the magazine article about ‘representing by means of dolls’. Besides the various modelmaking movements mentioned above, another part of the context is the scientific research community, which was distinct, as an institution, from self-appointed researchers such as the Wright Brothers and Otto Lilienthal. Yet, in terms of individuals participating in the activities, there was extensive interlacing between such institutions and communities; here Boltzmann’s interest in Lilienthal’s gliders is a good example. One formal such crossover was Edgar Buckingham, a physicist at the National Bureau of Standards in Washington, DC, who was loaned to the US Advisory Committee on Aeronautics. In particular, the year 1914 was a year especially marked by advances in research using scale models, theoretically as well as practically; in my paper ‘Physically Similar Systems: a history of the concept’ (Sterrett 2017a) I called 1914 ‘the year of physically similar systems’ due to there being so many publications germane to the topic appearing that year in the UK and in the US. One of these was the relatively understated, straightforward presentation of the foundations of the methodology of experimental (scale) models that Buckingham wrote in a publication that had been created to disseminate short communications about research of especial and/or urgent importance, sent out from US to other countries; the Journal of the Washington Academy of the Sciences; after that year, it became the Proceedings of the National Academies of Sciences, which is eminent to this day. Buckingham’s short communication published in July 1914 was under the PHYSICS rubric, and was entitled ‘Physically Similar Systems’. Reading the literature of that era, it is clear that news about technology and, especially, about aeroplane technology in 1914, was eagerly and urgently exchanged across borders and oceans—remember, there had already been a ‘Victorian Internet’ for quite some time by then—a transatlantic cable and an extensive network of electronic telegraph communications, and publication channels to disseminate the news were in place. (Standage 1998) So research in Washington DC easily made its way to Vienna where Wittgenstein was in mid-1914, practically instantaneously when necessary, and on a regular basis via such formal channels, as well as by more informal means. And, there were many other important publication events related to the topic that year; practically one per month [Sterrett 2006; Sterrett 2017].

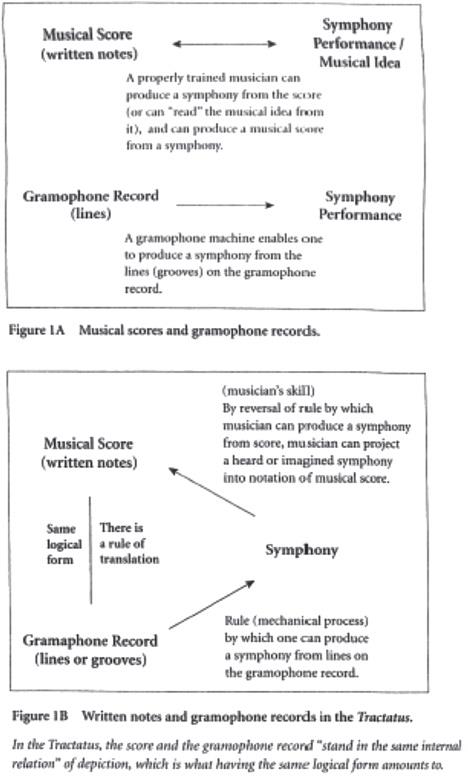
How did the events of 1914 figure into the writing of the Tractatus? That is, what difference is due to whatever important insight was gained in 1914? I provided a sort of answer to this in my book. Illustrating with figures, I showed how two important discussions of how a proposition depicts given in the Tractatus—(i) of the proposition as a picture, and (ii) of gramophone records and a symphony score having the same logical form—underwent development during the war, based on the Notebooks Wittgenstein kept during the war. I also provided some historical scientific and technological context crucial to understanding his use of gramophone records in the latter discussion.

Here I’ll refer to the figures presented in my book, Wittgenstein Flies A Kite: A Story of Models of Wings and Models of the World [Sterrett 2006] to illustrate how the events of 1914 discussed above figured into the writing of the Tractatus.

The juxtaposition of sketches portrays the development of two-part accounts into three-part accounts, which occurred during the war. Juxtaposing Figures 1A and 1B shows that the pre-1914 view of a symphony (the two two-part sketches in Figure 1A) is developed into the post-war view in the Tractatus (the three-part relation in Figure 1B). Juxtaposing Figures 2A and 2B with Figure 4 shows that the pre-1914 view of propositions (the two two-part sketches in Figures 2A and 2B) is developed into the post-war view in the Tractatus (the three-part sketch in Figure 4).

Thus, the sketches that portray the two (post-war) views of themes (i) and (ii) I find in the Tractatus (of the proposition as a picture and of the gramophone record and symphony score having the same logical form, respectively) are Figure 1B and Figure 4, respectively.

As I see it, there is a development of the two themes (i) and (ii), as follows:

— Prior to mid-1914, Wittgenstein would have had experiences with the fairly new technology of producing music from the grooves of a gramophone record, and, due to the family he grew up in, was party to many critical conversations about the nuances of producing music from musical scores via musicians’ performances (whether by playing an instrument, or by voice/whistling). This is shown on Figure 1A from my book: basically, what the sketches in Figure 1A depict is that a properly trained musician can produce a symphony from the score (written in musical notation); and that at least some musicians can also produce a musical score from hearing a symphony. In addition, Figure 1 depicts that a gramophone machine enables one to produce a symphony from the lines on a gramophone record. (There is no mention of the symphony performance producing a gramophone record, though.) It is interesting that the technology of recording sound in lines was developed years before this—the phonautograph, which produced records that were valued as two-dimensional visual records of sound, without any interest in their value as means of producing/reproducing sound. (Sterrett 2006; Sterne 2003; Sterne & Akiyama 2012) The phonautograph was very well-known as a scientific device; it is reported that every schoolchild read in their science textbook how a phonautograph could produce these visual records of sound, and that the nature of sound could be studied from these visual records. As for the possibility of producing sound from these graphical or visual records, the inventor of the phonautograph showed only scorn at what he regarded as the trivialization or vulgarization of his invention. Thus I take Wittgenstein to be knowledgeable of both phonautographs and gramophones, and that in choosing to mention the gramophone, rather than the phonautograph, he means to refer to the process of producing sound from the lines on the gramophone record.

— Also, prior to mid-1914, in the pre-war Notes on Logic, Wittgenstein had worked out a view about the relationships between propositions, signs, and symbols. The pre-war view is shown on Figures 2A and 2B (reproduced from Sterrett 2006). So, he already had that much, well before the insight in Autumn 1914: i.e., he had already said that the correspondence between a propositional symbol and reality depends on the simples that the symbol contains, and ‘that a certain thing is the case in the symbol says that a certain thing is the case in the world’. He had written, regarding propositional signs, that ‘if an x stands in the relation R to a y the sign “xRy” is to be called true to the facts and otherwise false’. He had written, regarding the human skill of understanding propositional signs, that ‘I understand the form “xRy” when I know that it discriminates the behavior of x and y according as these stand in the relation of R or not’. And, regarding propositional truth functions: ‘In two molecular functions that have the same T-F schema, what symbolizes must be the same’.)

So he already had that much; what happens after the crucial insight in Autumn of 1914 gets developed?

One thing to take note of and reflect upon is that Wittgenstein focuses on pairs of seemingly dissimilar representations: ‘At first sight a proposition— one set out on the printed page, for example—does not seem to be a picture of the reality with which it is concerned. But neither do written notes seem at first sight to be a picture of a piece of music, nor our phonetic notation (the alphabet) to be a picture of our speech.’’ (4.011) Now, notice: He does not appeal to examples in which similarity is based on visual or geometrical similarity. That’s very important. It is often missed.

— In the Tractatus, as depicted in Figure 1B, the lines on the gramophone record, and the musical notation of the symphony score, which Wittgenstein describes as two things which ‘appear to be very different at first’, are shown to ‘stand in the same internal relation’ of depiction, which is what having the same logical form amounts to. (Sterrett 2006; 216) His account of having the same logical form involves processes that result in a musical performance: the musician’s abilities in being able to ‘obtain the symphony from the score’ and the ability to employ a process that likewise yields the symphony from the lines on a gramophone record. This is what having the same logical form amounts to: translatability, though by no means a direct correspondence between points on the gramophone lines and notes in the symphony score.[xii]

It’s worth emphasizing here again that Wittgenstein did not appeal to the geometric characteristics of the lines on the gramophone record, even though, in his day, the patterns that the lines that a musical performance recorded on a gramophone disc or roll made were often appreciated as two-dimensional drawings (such as magnified traces of wavy lines made by a phonautograph needle used to record voices and other sounds. Likewise, in physics, Mach’s famous schlieren photographs capturing shock waves visually were widely reproduced and had become part of popular and artistic culture.) The gramophone example is used to make a point about propositions: ‘A gramophone record, the musical idea, the written notes, and the sound-waves, all stand to one another in the same internal relation of depicting that holds between language and the world’. [T 4.014] What they all have in common, though, he says is ‘logical structure’ [Ogden translation]

If geometric or visual similarity is not what Wittgenstein appeals to in explaining that the musical score and the lines on a gramophone record have the same logical form, what does he appeal to? Intertranslatability via serial processes. The processes he appeals to include ones that involve skill, training, and conventions about notation, as well as some mechanical processes. This is, I think, a very important thing to notice. It does not mean that those spatial relations or visual similarity do not play some role in the processes of translation, but the account of logical form is not in terms of, and certainly not reducible to, them. Here I suspect Wittgenstein is following Frege in thinking that it is the notion of translation, rather than the notion of interpretation, that is relevant in understanding logical form. In his criticisms of formalism in mathematics, Frege argued against the use of uninterpreted formulae in mathematics and logic. (Sterrett 1994) (We are not always careful in distinguishing the terms; for Frege, translation is from one meaningful entity to another; interpretation, as the formalists meant it, was from one uninterpreted statement to an interpreted one.)

How is the account of logical form that appears in the discussion of the gramophone in the Tractatus related to the experience of reading about a miniature setup used in a courtroom to portray something about a traffic accident?

Models in a Nexus of Fault and Responsibility

It would be nice to know a little more about how the miniature setup of the traffic accident was discussed in the magazine or newspaper that Wittgenstein read; what kind of evidence was the miniature setup supposed to provide? The setting was a law court, not a scientific laboratory or even a forensic one. The miniature automobiles involved in the setup are often referred to as ‘toys’ by commentators on Wittgenstein, though I am not aware that Wittgenstein ever did so in his Notebooks.

The miniature cars involved may well have been regarded as toys by some, but we have seen how exquisitely detailed technically many of them were. We have seen that in the late nineteenth and early twentieth century, scale models that were serious affairs and scaled to be used as experimental models for particular scientific research or forensic investigative purposes were often called toys, too. We have seen that modelmaking combined art and science, and that by 1914 there were modelmaker hobby clubs and ‘modelmaker’ was a skilled profession in the UK and the US—and that these kinds of miniature models with exquisite technical detail were known in Europe as well. Even rigorously scaled models were sometimes made to be aesthetically pleasing as well as being precision pieces of machinery. Modelmakers of such charming models were known to protest that calling their productions toys failed to do justice to the craftsmanship, knowledge, and precision required in order to produce properly scaled behaviors. Different materials had to be used to provide appropriately scaled densities and flexibilities; surfaces had to be modified to give appropriately scaled mechanical behaviors. So I think one point to keep in mind is that someone with Wittgenstein’s knowledge and interests in aeronautical engineering, in which precision scale models were absolutely essential, could hardly suppress knowledge of the logical and mathematical basis for using scale models in physics, when viewing such a miniature setup.

There are some cultural and ethical aspects to the significance of such a court case around 1914, too.

First, the issues of the burden of proof for proving fault in automobile accidents, and whether injury and death caused by automobile accidents should be covered under criminal law or not, were still undergoing change and clarification. There were even questions of ethics involved as to what kinds of considerations were relevant in applying the existing legal doctrines to the situation of automobile accidents (e.g., consideration of risk spreading; role of ownership, role of vehicle being under one’s control, role of negligence). (Deak 1931) This might be something to keep in mind with respect to Wittgenstein’s later remark that the most important point of the Tractatus was an ethical one—what it did not say.

Secondly, it is also significant that, in 1914, an important revolution in the use of physical evidence in court cases that would set the agenda for methods used in forensic investigation to this day, was just beginning. The Frenchman Edmond Locard, a protege of Bertillion who claimed to have used the fictional Sherlock Holmes as his inspiration and guide, had just been given a laboratory in Lyon (France) in 1912 in rooms attached to the courthouse, for such scientific investigations. The question of what kind of physical evidence could be admitted, and what it could be used to prove, was of interest to the public, as it hadn’t really been settled yet. Other laboratories were established based on Locard’s methods: first in 1914, there was one in Quebec (Cimon 2014); many others followed. Locard is known best for the methods he developed and disseminated using the microscope for making minute distinctions, such as between many different kinds of dust particles, and, following his teacher Bertillion, for the use of various biometrics for all sorts of imprints a person might leave behind. (Berg, 1970) However, Locard was also very much interested in collisions; in his laboratory in Lyon he worked on detecting cause and fault in automobile collisions: what did the evidence left behind from an automobile collision, such as skid marks left by tires, tell people about the collision that had taken place? This is a matter of reading the collision from the skid marks, but in a courtroom, one would also want to show how the skid marks could have been created by a certain sequence of events that was the fault of one of the drivers. Could one and the same model have served both to illustrate something such as who had the right of way and also to prove that skid marks (lines) left on the road could be translated into a certain sequence of events?[xiii]

Referring again to the illustration in the magazine article I found showing a personal-injury lawyer seated at a table on which a large piece of paper covering the entire tabletop has been lain: note that the outlines of the roads leading into an intersection are sketched on the paper. Five ‘miniature’ vehicles are on the table; although referred to as ‘miniatures’ in the article, they are large miniatures: most of the automobiles must be at least the size of a breadbox, it appears to me, and they look quite detailed. There are several doll occupants in the vehicles, and they seem arranged with care, in different postures; some are unprotected, their vehicles being open like a convertible. One three wheeled vehicle is toppled. The account says that the lawyer is ‘studying a case to place the responsibility for the accident’ and to get ‘a clear idea of the different phases’ of it. We are told that he acts out ‘the whole occurrence’ so that ‘the questions of right of way, traffic regulations, rules of the road, and such matters’ are made clear. The lawyer also uses the model to communicate: ‘Thus equipped, he is able to place his case lucidly before the court’. (Popular Science 1914) This account seems to fit with Wittgenstein’s mention of dolls (Puppen); it is the injury to the humans that is of most importance to the personal injury lawyer. This account also fits well with von Wright’s description that ‘At the trial a miniature model of the accident was presented before the court. The model here served as a proposition; that is, as a possible state of affairs.’ (von Wright n.d, p. 21)

One striking (to me[xiv]) thing is the context of this ‘found object’ (the model of a traffic accident): a court of law. Much of what the lawyer wants to present using the model involves conventions and, especially, violations of ‘traffic regulations’ and ‘rules of the road’. The physical aspects of the model are surely part of judging whether there have been violations, as well as in determining the sequence of events that led to an injury, and to how the injury was caused. But whether there have been traffic violations, and who had the right of way, involves rules and conventions as well. In the Notebooks, in following up on his thoughts about a proposition as a picture, Wittgenstein remarks that a picture might be used to portray how not to fence. (Wittgenstein 1979, NB 5 November 1914 entry) The model might be used to portray a violation of a traffic rule, or it might be used to portray a state of affairs that did not occur, say, in showing negligence, to show what would have happened (a possible state of affairs) had a driver acted otherwise than he or she did.

Another striking thing in the account of the model of a traffic accident in this magazine article is the mention of the dynamics of the model: ‘the different phases’; ‘the whole occurrence’, which draws attention to the miniature model of the traffic accident as a dynamic model. There is, after all, a vehicle that has been overturned, and one that is in the process of turning a corner. Certainly the way the lawyer is using the model is, at first, investigatively, or experimentally, to examine the situation and the possible ways it might have developed to yield the outcomes known to have occurred, and the possible ways it could, counterfactually, have developed.

As I explained in my book, what I see in the Tractatus is an account of how propositional sign, truth function, and world are related that looks very much, even in details, like an analogue of the account of using model experiments—e.g., ships, aeroplanes, propellers—to represent actual or imagined ships, aeroplanes, and propellers circa mid-1914. Actually, the methodology used—physically similar systems—is very general. The quote from Hertz’ preface that the form we give our images in thought is such that ‘the necessary consequents of the images in thought are always the images of the necessary consequents in nature of the things pictured’[xv] is often cited in connection with Wittgenstein’s Tractatus, but I do not think Hertz meant to be saying anything novel with that statement in the preface; statements to that effect are quite common in nineteenth century physics. The idea that one can formulate a picture or model—a concrete physical setup as well as an imagined or mathematical one—and set up a correspondence between them such that the consequents of manipulating quantities in the model that correspond to the thing modeled are the corresponding consequents in the thing modeled was also quite common. When it was an equation rather than a physical model, and the consequent a matter of mathematical deduction, Hertz’ statement would fit, too. The use of dimensionless parameters as a criterion for this kind of similarity between two physical systems—i.e., similarity of systems S and S’ (which is the terminology used to describe the relationship between a model being tested experimentally and the thing it modeled) exists when the relevant dimensionless ratios formed from the corresponding quantities in the two systems are equal—was also developed in physics in the second half of the nineteenth century. What I often found, though, was that mathematicians, physicists or engineers writing about similar systems and similarity would often comment that the methods were not well enough known, that they were powerful and elegant and that there was much to be gained by adopting them. (Sterrett 2017a)

Experimental Models and Measurement

What happened in July 1914, with the ‘Physically Similar Systems’ short communication (Buckingham 1914) was significant, though, in that the method was generalized so that it no longer involved deriving the required criteria from an equation that described the phenomenon. Rather, similarity criteria (the dimensionless ratios that must have the same value in each of the two systems (model and thing modeled)) could be derived from the ‘most general form’ of a physical equation, which contained no arithmetical constants. The most general form of a physical equation was written using the notation of functions. This often sounds not really possible; where does the information come from, if not from an equation of physics such as a partial differential equation? The reason it is possible is due to what is built into the system of measurement (as explained in Sterrett 2009; 2017a; Sterrett forthcoming b). It is the July 1914 formulation of similarity between physically similar systems as a methodology of using model experiments, that I use to draw the analogy shown by comparing Figure 3, below, with Figure 4 (above); the analogy is between experimental models and propositions in the Tractatus, respectively.

Beyond exhibiting the sketches in Figures 3 and 4 from my book here, I am not going to lay that analogy out again in this talk, as it is given in my book. I’d like to point out, though, some of the historical and biographical details supporting this suggestion. Here are just a few such details: Most saliently, the topic of similarity in science and engineering was prominent in the years immediately preceding 1914, and the short communication ‘Physically Similar Systems’ (Buckingham 1914) came out when Wittgenstein was already back from Norway, and staying in Vienna, where access to scientific news and literature was excellent. A timeline in my ‘Physically Similar Systems: A History of the Concept’ (Sterrett 2017a) shows the intensity of publications related to similarity throughout 1914. I cite lots of other supporting details in the book. Another one quite close in time to the 1914 insight was that the use of mechanical similarity was cited in a Nobel Prize Lecture given in December 1913 that received wide coverage in the Press, including cartoon caricatures of the Nobel Laureate, Heike Kamerlingh Onnes, as ‘Dr Zero’ in newspapers and magazines (the Prize was for achieving the liquefication of helium). Wittgenstein was in Vienna during that time period, too; even though he had been in Norway in 1913, he came back to his family home in Vienna for Christmas of 1913. Onnes had helped derive a more general ‘theory of corresponding states’ in physical chemistry than van der Waals’ initial version and cited Newton’s theory of mechanical similarity with awe. Wittgenstein could hardly have missed the association of Onnes’ work with model experiments, as Newton and, to some extent, Galileo, were often cited in the scientific and engineering literature on using experimental models as the first to use and write about similitude. With regard to the homage to Newton, as I have explained above and noted in my book (Sterrett 2006), the recently discovered fact that Wittgenstein purchased exactly the two works by Newton and Galileo that were cited in the literature on dynamic similarity and physically similar systems seems to indicate an awareness of the kinds of allusions Onnes and others made regarding the theoretical foundation for similarity in physics.

Models, Physically Similar Systems, and the Tractatus

These historical and biographical facts are merely supportive, though, as opposed to propelling me towards the conclusion initially: my main reason for thinking that the methodology of physically similar systems, which by the time of Wittgenstein’s reading of the magazine article in September 1914 had just been presented in the short communication ‘Physically Similar Systems’ (July 1914), is in fact the analogy itself that holds between the account of how models portray in it, and the account of a proposition given in the Tractatus. In particular, the ‘no logical constants’ principle that Wittgenstein referred to as the Grundgedanke of the Tractatus has a clear analog in the account (i.e., equations in science that contain arithmetical symbols are replaced by ones that do not contain any such connectives, by employing functional notation). Most significantly, the analogy yields an account of objects that I find aligns perfectly with the statements in the Tractatus about objects and facts composed of objects, sans logical constants. Whereas the methodology of experimental models speaks of the ‘most general form of a physical equation’ as containing no algebraic constants, Wittgenstein writes of the ‘general form of a proposition’ containing no logical constants.

— Whereas, in the dimensional equations used in Buckingham’s July 1914 ‘Physically Similar Systems’ paper, dimensions or quantities combine in only certain ways to form dimensionless parameters, in the Tractatus we are told that objects combine in only certain ways to form ‘states of affairs’.

I see the way objects function as completely analogous to the way that dimensions do.

One thing that is not shown on the figures in my book is how the elements in the model correspond to the elements in reality. This is very straightforward, although implicit: since the similarity of the two systems is a matter of certain key dimensionless parameters (ratios) having the same value in the model as in the thing modeled, one can simply show the correlation between model and thing modeled from those ratios alone. To take an easy case, consider Mach number, a degenerate case[xvi] of a dimensionless parameter: (velocity of a moving body v)/ (velocity of sound in the fluid at the fluid conditions that obtain vs). Suppose we have a case in which similarity is established by the Mach number being the same in the model as in the thing modelled (again, a degenerate case). Then, letting v depict the velocity in S and V depict the velocity in S’, we can say that v/vs = V/Vs We can then say that the velocity v corresponds to the velocity V vs/Vs; this gives the model its ‘feelers’, which shows exactly how the velocity in the model corresponds to the velocity in the thing modeled. Measuring one of these two velocities can be used to tell us what the other, corresponding, velocity is. With this in mind, we can make good sense of the following statements in the Tractatus (Wittgenstein 1974):

2.1511 That is how a picture is attached to reality; it reaches right out to it.

2.1512 It is laid against reality like a measure.

2.15121 Only the end-points of the graduating lines actually touch the object that is to be measured.

2.1513 So a picture, conceived in this way, also includes the pictorial relationship, which makes it into a picture.

2.1514 The pictorial relationship consists of the correlations of the picture’s elements with things.

2.1515 These correlations are, as it were, the feelers of the picture’s elements, with which the picture touches reality. (Wittgenstein 1974)

And, as for the statements following just after the above lines in the Tractatus, the ones about the picture having something in common with what it depicts: clearly, though we do not need to be using the same units in the model and what it models, the systems of measurement need to have some things in common (e.g., we need to be using the same system of measurement between the model and the thing modeled (not necessarily the same system of units, but of the same system of measurement) in order to use this method to construct a model that is able to picture what it models. (Sterrett forthcoming b) So, that makes sense too. (Exactly what they must have in common is, I think, part of the investigation in the Tractatus.)

Who Can Understand the Tractatus?

While I don’t want to repeat the arguments in the book here, I would like to point out that the analogy I laid out in the book (depicted by the juxtaposition of Figures 3 and 4) addresses what I think is a common worry about what’s known as Wittgenstein’s ‘Picture Theory’. The worry, I think, is that just knowing that the elements of a picture correspond to elements in reality doesn’t yield enough to guarantee that the picture will track reality. ‘Having the same logical form’ just seems too scanty a basis to most people, I suspect. Then, there is the problem with the point that, as Wittgenstein says, ‘The possibility of propositions is based on the principle that objects have signs as their representatives’. I think readers are bound to ask how this is supposed to be guaranteed, too.

I consider some of these worries to be genuine worries about endorsing what commentators call the Picture Theory—at least the Picture Theory as it is often understood. I don’t think it is very easy for a reader of the Tractatus to understand how the proposition as a picture is supposed to account for what it purports to account for in any rigorous way. In fact, I think Wittgenstein knew others weren’t going to understand his point, yet, that he felt that what he wrote was correct. He did, after all, write in the preface that, although he wasn’t sure he had accomplished the task of expressing the thoughts expressed in the book very well, that ‘the truth of the thoughts that are here communicated seems to me unassailable and definitive’. (Wittgenstein 1974, pgs. 3–4) I’m going to go with that line: Wittgenstein didn’t count on anyone being able to understand the thoughts he tried to express in the Tractatus, yet he thought the truth of those thoughts was ‘unassailable and definitive’.

I find that the key to making sense of the thoughts he attempts to express in the statements in the Tractatus about objects, states of affairs, and propositions is to recognize that his account draws on the existence of quantitative science, i.e., the existence of measuring systems and equations that express relationships between measured quantities. It is in the design and standardization of systems of measurement—which, in a coherent system of measurement, include a connection to reality, as a coherent system of measurements[xvii] requires that the units that have different dimensions associated with them be ‘coherently’ related to each other, which involves establishing physical relationships; as a result, the relationships between dimensions (kinds of quantities) are formalized. Since I see dimensions as analogous to objects, this explains many of the otherwise inscrutable claims about objects we find in the Tractatus.

Again, the historical and biographical details are supportive of my suggestion. First, there is the context that, in 1914, many physicists and engineers would know what a dimension was, and would be quite competent in using dimensional equations. They would consider it quite natural to think of combining dimensions, which can be done without any arithmetical connectives, and which come into play when expressing a dimension in terms of combinations of others. I say this because significant debates on the topic of which units should be used in physics were still in very recent memory in 1914; and these debates required the language of dimensions. In fact, Hertz had entered the debate with a very philosophical argument; Jed Buchwald discusses it in his book The Creation of Scientific Effects (Buchwald 1994, Chapter 12) In his argument, Hertz uses the notation of dimensions, i.e., he writes ML²T² to indicate the dimensions of the units of work; M, L and T denote respectively the dimensions Mass, Length and Time.

I think of a dimension as a kind of quantity. But—and this might have been difficult for even scientifically trained commentators and readers of the Tractatus coming upon it after 1930 or so to imagine—not only the system of units but the issue of how many basic units were needed in order to be able to do physics, was in flux in the late nineteenth century. There were the basic units of mass, length, and time, as in Newton’s day, but there was the new question of how to handle units for measurements made of quantities regarding electricity and magnetism. It was easy enough to define units of each, in terms of a laboratory procedure involving an electrical or magnetic pole. But, it was impossible to answer: ‘Which is more basic: an electrical pole or a magnetic pole?’ Contradictions arose no matter which system of units was preferred; in addition, many additional units were added and adopted, without increasing the number of basic units, because they were more practical to use. Some argued that three basic units (mass, length, and time) were sufficient. It wasn’t until 1901 that the Italian Giovanni Giorgi showed that by adding a fourth basic unit, and hence admitting a fourth dimension (a fourth basic kind of quantity) to the system of units, that the global physics community could solve the problem in an especially desirable way, in that the resulting system of units would not conflict with the use of the practical units already used in everyday technological and laboratory work. In 1914, though, these had not yet been adopted formally. The topic was still alive, and so was the language that was then considered the language of science: dimensional analysis. And, we do see Wittgenstein bring up measurement, as in his statement quoted above, that a proposition is laid against reality like a measure.

Secondly, I don’t think Wittgenstein says nearly enough to explain what’s needed to the reader who does not know very much about model experiments, dynamical similarity, and similar systems. In his defense, someone writing in 1914, which I have called ‘The Year of Physically Similar Systems’ (Sterrett 2017a), coming on the heels of Onnes’ fame, might assume that the whole family of similarity concepts had finally won the day in physics and were going to be as common as the notion of gravity from now on. That is what Boltzmann foresaw (Sterrett 2006, p. 113; Boltzmann 1974). Sadly, the opposite happened and the war seems to have disrupted collective memory about them.

Also, the arguments about the basis for measurement in the new physics, and the role of measurement standards in physics, had basically been made. It is true that, in 1914, it would still be a while before the solution Giorgi proposed around 1900/1901 was eventually adopted by the international agencies charged with deciding such things—but the debates that delved into the fundamental questions of measurement in electromagnetism, were over. So, even though there would still be active discussion of them in 1914, and the language of dimensional analysis would then still be quite well known, the occasions for using it in debates in which the question of how many different dimensions were needed was a live question were fewer and fewer. The result is that we philosophers are put in a deficient position with respect to understanding comments about measurement and modeling unless we are willing to go back and learn what physics was like in 1914—and I don’t mean current reconstructions of what was known in 1914 phrased in anachronistic terms.

So, I’d like to make a suggestion about understanding Wittgenstein’s Tractatus, at least the parts of it associated with the so-called ‘Picture Theory’: I suggest that it might help if we as a philosophical community get to know the scientific milieu in which the Tractatus was conceived a little better, including the language and methods of physics of the day. Especially, the language and methods, including systems of measurement, of the (physics) logic underlying the use of model experiments.

References

Anonymous (1914). ‘Lawyer Studies Accident with Plat and Toys’, Popular Science, June 1914: 819.

Berg, Stanton O. (1971). ‘Sherlock Holmes: Father of Scientific Crime and Detection’, Journal of Criminal Law, Criminology & Police Science, 61: 446–452.

Blackmore, J.T. (1995). Ludwig Boltzmann, His Later Life and Philosophy, 1900–1906. Book One: A Documentary History. Boston Studies in the Philosophy of Science, Vol. 168. Kluwer Academic Publishers.

Boltzmann, Ludwig, (1974). McGuinness, B.F. (Ed.) Theoretical Physics and Philosophical Problems: Selected Writings (Vienna Circle Collection). Boston, MA: D. Reidel.

Buchwald, Jed Z. (1994). The Creation of Scientific Effects. Chicago: University of Chicago Press.

Buckingham, Edgar (1914). ‘Physically Similar Systems’, Journal of the Washington Academy of the Sciences, 4: 345-376.

Cimon, Denis, Desharnais, Brigette & Dicaire, Catherine (2014). ‘One hundred years of forensic sciences in Quebec: the evolution of scientific techniques since 1914’, Canadian Society of Forensic Science Journal, 47 (3): 148–169.

Dahmen, Silvio R. (2009). ‘Boltzmann and the Art of flying’, Physics in Perspective, 11: 244–260.

Deak, Francis (1931). ‘Automobile Accidents: A comparative study of the law of liability in Europe 1931’, University of Pennsylvania Law Review and American Law Register, 79: 271–305.

de Clark, Sybil G. (2016). ‘The dimensions of the magnetic pole: a controversy at the heart of early dimensional analysis’, Archive for the history of the exact sciences, 70: 293–324.

de Clark, Sybil G. (2017). ‘Qualitative vs quantitative conceptions of homogeneity in nineteenth century dimensional analysis’, Annals of Science, 74: 299–325.

Hansluck, Paul N. (1902) The Model Engineer’s Handybook, A Practical Manual on Model Steam Engines Embracing Information on the Tools, Pictures, Models and Measures. Materials and Processes Employed in their Construction. London: Crosby, Lockwood, and Son.

Hertz, Heinrich (1956). The Principles of Mechanics. New York, Dover: D.E. Jones & J.T. Walley. Hide, Oystein (2004).’ Wittgenstein’s Books at the Bertrand Russell Archives and the Influence of Scientific Literature on Wittgenstein’s Early Philosophy’, Philosophical Investigations, 27: 68–91.

Janik, Allan and Toulmin, Stephen (1973). Wittgenstein’s Vienna. New York: Simon & Schuster.

Klagge, James C. (2001). Wittgenstein: Biography and Philosophy. Cambridge: Cambridge University Press.

Klagge, James C. (2016). Simply Wittgenstein. Online edition Simply Charly.

McGuinness, B.F., Ed. (2008). Wittgenstein in Cambridge: Letters and Documents, 1911–1951. Blackwell.

McGuinness, B.F. (1988). Wittgenstein: A Life: Young Ludwig 1889–1921. Berkeley: University of California Press.

Mitchell, Daniel Jon (2017). ‘Making Sense of Absolute Measurement: James Clerk Maxwell, William Thomson, Fleeming Jenkin, and the invention of the dimensional Formula’, Studies in History and Philosophy of Modern Physics, 58: 63–79.

Scott, Janny (2011). A Singular Woman: The Untold Story of Barack Obama’s Mother. New York: Riverhead Books/Penguin.

Standage, Tom (1998). The Victorian Internet: The Remarkable Story of the Telegraph and the Nineteenth Century’s On-line Pioneers. New York: Bloomsbury.

Stern, David G. (1995). Wittgenstein on Mind and Language. New York: Oxford University Press.

Sterne, Jonathan (2003). The Audible Past: Cultural Origins of Sound Reproduction. Durham, N.C.: Duke University Press.

Sterne, Jonathan & Akiyama, Mitchell (2012). ‘The Recording That Never Wanted to Be Heard and Other Stories of Sonification’, In Pinch, Trevor & Bijsterveld, Karin, Eds. The Oxford Handbook of Sound Studies, 544–560, Oxford & New York: Oxford University Press.

Sterrett, Susan G. (1994). ‘Frege and Hilbert on the Foundations of Geometry’, available at philsci-archive.pitt.edu/723.

Sterrett, Susan G. (2000). ‘Physical Pictures: Engineering models circa 1914 and in Wittgenstein’s Tractatus’, long version at philsci-archive.pitt.edu/661/1/ Sterrett-UNC-CH-PPTalk2.pdf.

Sterrett, Susan G. (2002). ‘Physical Pictures; Engineering models circa 1914 and in Wittgensteins’s Tractatus’, In Heidelberger, M. & Stadler, F., Eds., History of Philosophy of Science: New Trends and Perspectives, Vienna Institute Yearbook 2001: 121–135.

Sterrett, Susan G. (2005). ‘Pictures of Sound: Wittgenstein on Gramophone Records and the Logic of Depiction’, Studies in History and Philosophy of Science, 36: 351-362.

Sterrett, Susan G. (2006). Wittgenstein Flies A Kite: A Story of Models of Wings and Models of the World. New York: Pi Press/Penguin.

Sterrett, Susan G. (2009). ‘Similarity and Dimensional Analysis’, In Meijers, A., Ed., Handbook of the Philosophy of Science, Volume 9: Philosophy of Technology and Engineering Sciences, 799–824, Amsterdam: Elsevier/North Holland.

Sterrett, Susan G. (2017a). ‘Physically Similar Systems: A History of the Concept’, In Magnani, L. and Bertolotti, T., Eds., Springer Handbook of Model-Based Science, 377–411, Berlin/Heidelberg: Springer-Verlag.

Sterrett, Susan G. (2017b). ‘Experimentation on Analogue Models’, In Magnani, L. and Bertolotti, T., Eds. Springer Handbook of Model-Based Science, 857–878, Berlin and Heidelberg: Springer-Verlag.

Sterrett, Susan G. (forthcoming a). ‘Theory of Dimensions’ In Knox, Eleanor and Wilson, Alastair, Eds., Routledge Companion to the Philosophy of Physics.

Sterrett, Susan G. (forthcoming b). ‘Relations Between Units and Relations Between Quantities’, In Schlaudt, Oliver, DeCourtenay, Nadine, and Darrigol, Olivier, The Reform of the International System of Units (SI): Philosophical, Historical, and Sociological Issues.

Von Wright, G.H. (n.d.). Wittgenstein. Minneapolis: University of Minnesota Press.

Walter, Maila L. (1990). Science and Cultural Crisis: An Intellectual Biography of Percy Williams Bridgman (1882–1961). Stanford: Stanford University Press.

Wittgenstein, Ludwig (1922). Tractatus Logico-Philosophicus. C.K. Ogden, Trans. International Library of Psychology, Philosophy and Scientific Method. London: Routledge.

Wittgenstein, Ludwig. (1974). Tractatus Logico-Philosophicus. Revised edition. D.F. Pears and B.F. McGuinness, Trans. London: Routledge.

Wittgenstein, Ludwig (1979). Notebooks 1914–1916, 2nd edition. G.H. von Wright & G.E.M. Anscombe, Eds. G.E.M. Anscombe, Trans. Chicago: University of Chicago Press.

[ii] Hamilton’s ‘Wittgenstein and the Mind’s Eye’ in Klagge, James C. (2001) Wittgenstein: Biography and Philosophy, Cambridge University Press discusses Wittgenstein’s time at the Technische Hochschule in Charlottenburg and so is another such contribution. Hamilton (2001) emphasizes the use of visualization in engineering and does not mention wind tunnels or experimental scale models. Hamilton (2001) puts a great deal of emphasis on the significance of the coursework at the THS in Descriptive Geometry, though fails to mention that Brian McGuinness had a decade earlier made the claim that the notion of ‘proposition as a picture’ owed much to reflection on Professor Jolles’ classes in Descriptive Geometry and Graphical Statics. (McGuinness 1988, p. 61).

[iii] As the online archive of HOPOS conferences and workshops does not at present include the year 2000, the abstract of my talk at HOPOS 2000 is not available on the HOPOS website. Hence, I provide it here: ‘’Physical Pictures: Models in Engineering Practice circa 1914 and in the Tractatus.’ In 1914, Wittgenstein recorded an incident in his Notebooks that he later mentioned to several friends as occasioning a major insight into his views in the Tractatus that propositions represent by being pictures. The entry reads: ‘In the proposition a world is as it were put together experimentally. (As when in the law court in Paris a motor-car accident is represented by means of dolls, etc.)’ This incident, he said, was pivotal in coming to the view in the Tractatus that propositions represent by being pictures. In his later writings as well, investigations of what it is to understand a proposition remain tied to investigations of what it is to understand a picture.

Numerous scholars have looked to Hertz’s Principles of Mechanics as the element of Wittgenstein’s milieu from which he drew the notions of model and picture used in the Tractatus; that they have done so may be due to a brief parenthetical remark in a much later section of the Tractatus. However, I think that a far more relevant source of a notion of model in Wittgenstein’s milieu was the engineering scale model. The methodology of scale modeling is strikingly different from analytical methods, in just those ways that are important to the notion of picturing found in the Tractatus: the primary notion is that of translatability between two physical situations, rather than between a physical situation and a mathematical or linguistic representation, or, even, between two physically similar situations whose similarity is established by showing that they are both instantiations of the same more general equation or general description. The notion fits well with the remark: ‘The essential nature of the propositional sign becomes very clear when we think of it made up of spatial objects (such as tables, chairs, books) instead of written signs (3.1.4.3.1)’ It’s also significant that the methodology of scale modeling can be used when one has no theory by which the behavior of the model can be predicted, or, even, a theory of the phenomenon being investigated.

Since wind tunnels were already in use in Germany when Wittgenstein did his engineering studies there, the concept of scale model would actually have been in the milieu much earlier than the pivotal 1914 notebook entry. However, the methodology of scale modeling was then more a matter of engineering practice than it was a formal methodology. At the time Wittgenstein recorded the insight about a world being ‘put together experimentally’, the field was at a threshold as far as the formalization of its methodology; logical and mathematical foundations of the practice were just then beginning to be developed. It was in 1914 that Buckingham’s proof about the minimum number of dimensionless groups needed to identify physically similar situations was presented in London. I’ll also explain why I think the use of a scale model in the context of a courtroom, rather than a laboratory, lent significance to the incident.’ (From: HOPOS 2000, Third International History of Philosophy of Science Conference, Vienna, July 6–9, 2000. Abstracts. Booklet with letterhead graphics for Institute Vienna Circle: Society for the Advancement of Scientific World View. Imprint: kognito Berlin Conference website: http://ivc.philo.at/hopos/2000.htm)

[iv] The closest analog I can think of in current society is the cultural phenomenon of computer games: there is a whole subculture built up around online computer games, and many different communities, clubs, events, and publications have formed around the activity of computer gaming. For children, the currently popular computer game Minecraft might be an analogue in some ways to the cultural phenomenon of model building in the late 19th and early 20th century.

[v] The presentation of the problem of heavier-than-air flight in Verne’s novel as a scaling problem much the same way Boltzmann presented it in his encyclopedia article, ‘Model’, is discussed in Sterrett 2006, p. 25 – 27.

[vi] As Wittgenstein was just about to leave research in aeronautics, an international cup (now known as the Wakefield Cup) for “aeromodels” was established, and was first awarded in April 1911 at a competition held in the Crystal Palace in London. One account is available at old.fai.org/f1-free-flight/wakefield-international-cup/427-ciam/ciam-f1/ciam-wakefield/33215-lord-wakefield-of-hythe-1880-to-1941

[vii] A discussion of this collection, with excellent photographs, is online at ‘Invention and the Patent Model’, The National Museum of American History at http://americanhistory.si.edu/invention-and-patent-model

[viii] ‘Modell-Flugvereine’, Deutsche Luftfahrer Zeitschrift, 20 Dec. 1916, p. 368. Smithsonian Collections Online, http://tinyurl.galegroup.com/tinyurl/5jzP75. Accessed 7 Jan. 2018.

[ix] Original in German. The translation is my own, with a few changes suggested by Jasmin Özel.

[x] Wittgenstein in Cambridge shows that ‘Letter to G E Moore’ [from Wittgenstein] has a return address from the house at Neuwaldeggerstrasse 38, on the outskirts of Vienna. (McGuinness 2008, p. 75)

[xi] http://www.wittgensteinchronology.com/7.html

[xii] There are a number of other relevant points associated with Figure 1B discussed in ‘Pictures of Sounds: Wittgenstein on Gramophone Records and the Logic of Depiction’ (Sterrett 2005)

[xiii] Here there is a very close analogy between the lines on the gramophone record that can be used to reproduce a symphony performance with some, but not perfect, fidelity, and the lines on the road that can be used to reproduce the scene of a traffic accident with some, but not perfect, fidelity.

[xiv] I mentioned it at the end of Sterrett (2000) ‘Physical Pictures: Engineering models circa 1914 and in Wittgenstein’s Tractatus; long version at http://philsci-archive.pitt.edu/661/1/Sterrett-UNC-CH-PPTalk2.pdf As for the more substantial content of the talk, the content in Sterrett 2006 supersedes that talk.).

[xv] Quoted in David G. Stern’s Wittgenstein on Mind and Language, p 37, from Heinrich Hertz: The Principles of Mechanics, Tr. by D.E. Jones and J.T. Walley. (Dover, New York 1956)

[xvi] I use here the simple case of Mach number, which I called a degenerate case of a dimensionless number, to illustrate how the corresponding quantities can be identified from the dimensionless ratios, to keep the calculation simple. A clear nontechnical description of ‘degenerate’ is ‘In mathematics, a degenerate case is a limiting case in which an element of a class of objects is qualitatively different from the rest of the class and hence belongs to another, usually simpler, class.’ (Wikipedia 26 January 2018) Mach number is a degenerate case of a dimensionless ratio in the sense that the only kind of quantity it contains is velocity, and hence is a limiting case of dimensionless ratios, which can contain many different kinds of quantities.

[xvii] There are two characterizations of coherence of a system of measurement; this is one of them. I discuss the topic at length in Sterrett forthcoming b (‘Relations Between Units and Relations Between Quantities.’)